化学に革命をもたらす”計算の力”──ICReDDが描く未来の反応地図（前編）
2025年09月10日掲載
AFIR法で見る化学の「地形」
かつて未知の化学反応を発見するとは、山奥に分け入り、道なき道を歩き回って落とし物を捜すようなものだった。研究者が自らの知識と経験を頼りに反応条件を考え、一つひとつ手探りで実験して試す他なかったからだ。
しかし今では地図のない土地にドローンを飛ばして地形をスキャンし、最適ルートを見つけ出すようなことが化学研究の現場で可能になった。
そんな革新的な探索を牽引しているのが北海道大学化学反応創成研究拠点（WPI-ICReDD）だ。その中でも注目されるのがICReDD拠点長で、理論化学者の前田理さんが開発したAFIR法（人工力誘起反応法）である。
ICReDD拠点長・前田 理（さとし）教授
量子化学計算に基づく反応経路自動探索手法であるAFIR法は、暗闇を照らすサーチライトの役割を果たす。
「化学反応経路を自動で探索することは絶対に不可能だと言われていました。25年前からその手法の開発に取組み、実験科学者にも有意義と思ってもらえる化学反応を示せるところまできました」（前田さん）
分子はその構造が変化（たとえば直線型からU字型へ変化）するとエネルギーが変わる。分子構造に対応するエネルギーの変化を表すのがPES（ポテンシャルエネルギー曲面）だ。PESは分子の形ごとのエネルギーを表す一種の立体地図だが、その中で標高が低い領域はEQ（平衡構造）と呼ばれる。EQは分子が安定して存在できる「盆地」。化学反応とは、詰まるところ、あるEQから別のEQへ移ることだ（図１）。
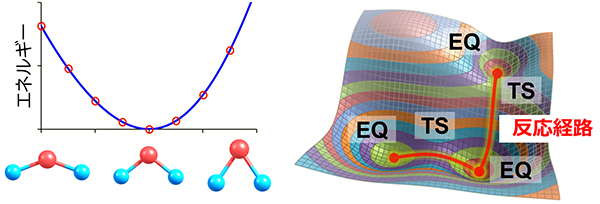図１）ポテンシャルエネルギー曲線（左）と、ポテンシャルエネルギー曲面（右）
ただしEQから別のEQの間はエネルギー障壁で隔てられており、簡単には移動できない。そこでAFIR法では、コンピューターの中で仮想的な外力（人工力）を分子のさまざまな部位に与えて、このエネルギー障壁を強制的に越えさせる。その結果、道筋＝反応経路が見出される。それは峠のように山頂と山頂に挟まれ、相対的に低くなった鞍部で、TS（遷移状態）と呼ばれる。
前田さんによれば、AFIR法とは「盆地から峠を通って別の盆地を結ぶ道筋を網羅的に見出す方法」だという（図２）。
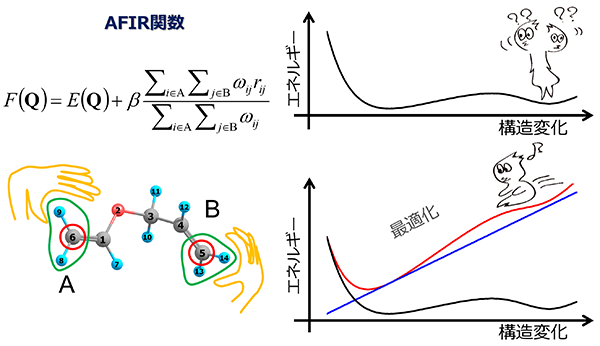図２）AFIR法の概念図。グラフ上ではゆるやかな上りに見える箇所は、化学反応の進行のために越えなければならないエネルギーの障壁。そこで反応物に仮想的な外力を加えて標高を高くしてやれば、まるで滑り台を滑るように、分子が安定する「盆地」（＝生成物）へとストンとたどり着く道が見出せる。
EQと別のEQを結ぶ反応経路が現実にあり得ることを数理的に裏づけるのが、量子力学の原理に基づいて分子の電子状態、構造、エネルギーなどを導き出す手法である量子化学計算である。
AFIR法では、分子の構造を変えるたび、反応経路を変えるたびに、EQと別のEQの間のエネルギーの傾き（勾配）を何度も計算する。そのおかげで網羅的に反応経路が見出されるのだが、その分、計算コストは高くなる。特に、探索対象となるEQが多く、反応の可能性が複雑に広がる系では、膨大な数の勾配計算が必要になり、計算時間やリソースの消費がボトルネックとなる。
反応の「速さ」に注目
勾配計算をいかに減らすか。もちろんやみくもに減らすわけにはいかない。求められるのは網羅的な反応経路の中から、非現実的な経路を除き、実際の条件下でたどり着ける可能性が高い経路だけを残す方法だ。
このような合理的な化学反応を予測する助けとなるのが、化学の伝統的な理論の一つ「速度論」だ。速度論では化学反応が起こるかどうかより、その反応がどのくらいの速さで進むかに注目する。「反応はたしかに起こる」としても、もしその反応が進行するのに100年かかるとか、極端な高温が必要なら、それは実質的に不可能ということだ。
しかし、速度論に基づく微分方程式を解こうとすると、その中に高速に変化する変数と、ゆっくり変化する変数が混在するため、数値的に解くことが極めて困難という課題があった。
突破口を開いたのが、前田さんの研究室に博士課程の学生として以前所属していた住谷陽輔さん（現・山口大学助教）を中心に構築されたRCMC法（速度定数行列縮約法）だ。
化学反応は、たとえば温度によって進行速度が変わる（温度が高い方が反応速度は速くなる）。RCMC法では、反応速度の指標である速度定数を使い、温度などの反応条件ごとに、AFIR法で網羅的に洗い出された各反応がどれくらい速く進むかという点から評価して、クラスタを形成し、簡略化する。ユーザーが時間スケールを任意に設定し、もし短時間で反応が進むのであれば、同じEQのクラスタとしてまとめるわけだ。それにより無駄な計算を省き、現実的に到達可能な反応経路に絞ることで、計算コストを下げることができる。
RCMC法を確立する上で、重要な役割を果たしたのはグラフ理論だ。EQをノード、TSをエッジと見なせばグラフ理論を適用できるからだ。EQからTSを介してEQへ至る無数の経路からなる複雑なネットワークを読み解くべく、前田さん、住谷さんは、情報科学・数理の専門知識を持つ小松﨑民樹さん（ICReDDのPI、教授）、当時小松﨑さんの研究室に博士課程の学生として所属していた永幡裕さん（現・小松﨑さんのグループのリサーチフェロー）とともにRCMC法を構築した。
「小松﨑先生と繋がる情報科学関連の研究会などにも参加させていただき、そういった機会を重ねていくうちに段々と化学反応経路ネットワークとグラフ理論をかけ合わせるアイデアが出来上がっていきました。」（前田さん）
RCMC法は理論化学と情報科学をかけ合わせることで生まれたと言える。その強みは、AFIR法が見出す無数の反応経路のうち、重要な反応経路の収率を出し、現実的に合成可能な生成物の候補や、反応条件を絞り込めるところにある。なお収率とは、化学反応において反応物からどれくらいの生成物が得られたかを表す割合、つまり、どれくらいうまく反応が進んだかを示す数値である。 「あらかじめ知られている反応なら、生成物の候補をピックアップして、そこに向かう反応経路の収率だけ出せばいいのですが、未知の反応を予測するには、すべての反応経路について、こちらには何％、あちらには何％と収率を割り当てる必要があります。反応経路を解析することはできるとしても、未知の反応を予測することまでは不可能と言われていましたが、われわれは実現しました」（前田さん）
速度論の応用により未知の化学反応の予測を可能にし、新たな化学研究の道を切り開いたRCMC法は、思わぬ分野にも波及効果をもたらしたという。
「数学です。RCMC法の中に、ある連立方程式を解く部分があるのですが、われわれはこれを化学の言葉で書かれたアルゴリズムにより解析できるようにしました。ところがこの連立方程式を数値的に解くのは数学的には難しいというのです。そこで2019年からERATOプロジェクトで副研究総括としてともに研究を進め、2020年からはICReDDのPIとして一緒に活動している、離散数理工学などを研究する数学者の岩田覚さん、大城泰平さんがわれわれのアルゴリズムを数学的な表現に書き直し、それによってより高速な解析が可能になりました」
数学者が数学的な興味で確立していた理論が、未知の科学的な現象を読み解くのに使われた例はいくつもある（有名な例はリーマン幾何学を利用したアインシュタインの一般相対性理論）。逆の例は珍しい。しかし化学反応とはある意味、自然が人間にはまだ知られていないルールまで使って問題を解く現象だ。化学的な言葉で書かれたアルゴリズムが自然の「解法」をより忠実に反映し、従来の数学を先取りすることもあり得るわけだ。
「北大にICReDDが設立され、長い間、化学者と数学者がタッグを組んで共通の課題に取組んできたからこそ、お互いにとって意義のある成果が出せました」（前田さん）
逆合成への挑戦
前田さんらは生成物から反応物を予測する技術「量子化学的逆合成解析（Quantum-Chemistry-aided Retrosynthetic Analysis: QCaRA）」も確立した（図３）。
QCaRAは、反応物から生成物を予測する代わりに、生成物から出発して、それを合成するにはどのような反応経路があり得るか網羅探索する手法である。料理の完成品から、どんな食材、香辛料などを使い、どう調理したかを推測するようなものである。
名店の料理を食べただけで、そのレシピを完璧に特定できる人は少ない。この種の逆問題を解くのは極めて困難だ。頂上は同じでも、上る道はさまざま。ある生成物に至る反応経路が無数に存在するのだ。
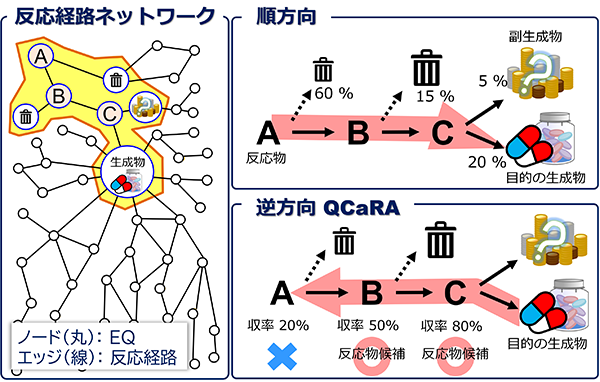図３）QCaRAの概念図。標的分子を入力とした逆探索による化学反応を予測する量子化学的逆合成解析が可能となった。
AFIR法を使えば、生成物から遡ってその前駆体の候補を探索できる。各候補からさらにその前の前駆体候補を網羅的に見つけていけば、ついには反応物に至るだろう。しかし、この方法ではあっという間に計算爆発を起こす。
ここでもRCMC法が活躍する。AFIR法で見つけた前駆体候補に至る経路において収率を計算し、それがゼロであるような経路は除去してしまう。現実に起こりうる反応だけを絞りこむのだ。RCMC法をうまく使うことによりQCaRAが確立された。
実験科学者の関心と現実
コンピューターが「発見」した反応経路は、実際にどれだけ役に立つのか。仮想世界の中にしか存在しない新しい化合物にはあまり意味がないように思える。
しかし、コンピューターが発見した未知の化学反応を実験科学者が実験で確かめる機会は滅多にないという。
「実験科学者のモチベーションの多くは、学会で発表して注目される化学反応を見つけることだと思います。コンピューターは、これとあれを混ぜたらこんなものができるという化学反応をたくさん出しますが、実験科学者に興味を持ってもらえるものはまだ少ない。有望な反応が予測されていても、その反応に必要な試薬がすぐには買えないようなものである場合も、実験のハードルは高くなる」（前田さん）
そんな中でも、実験科学者との融合研究が成果につながった例もある。その一つが、QCaRAによるα-アミノ酸の一種「α,α-ジフルオログリシン」の合成だ（図４）。
α-アミノ酸はペプチドやタンパク質を構成する生命の基本単位で、医薬品、食品、化粧品などに広く利用されている。特に、人工的に改良された「α, α-ジフルオログリシン」は、代謝安定性や生理活性を高める効果のあるフッ素を持つことから創薬などに役立つだろうと期待されてきた化合物だが、長らく効率的に合成する方法が知られていなかった。
前田さんらはQCaRAを用いて、この化合物を合成する反応経路を探索した。その結果、見出されたのが、ジフルオロカルベン、アミン、二酸化炭素という入手しやすい化合物を出発原料として合成する経路だった。
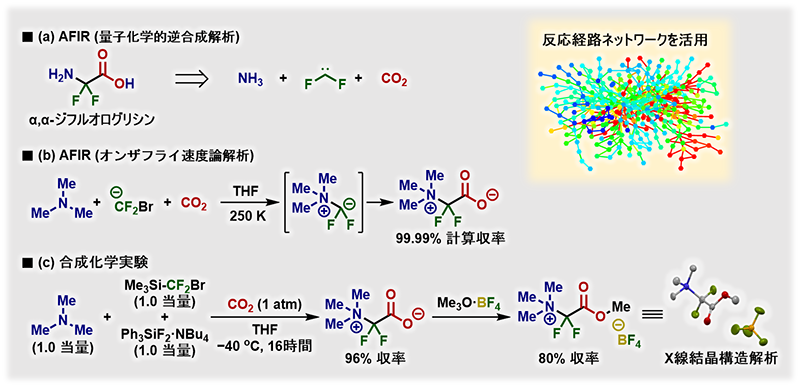図４）ジフルオログリシン誘導体合成法の開発手順 (Meはメチル基（CH3）の略)
ICReDDの教授で、有機合成化学を専門とする美多剛さんは、これらの化合物からα, α-ジフルオログリシンを高収率で合成に成功した。候補となる反応経路の発見から実際の合成までわずか2か月だったという。通常は新しい合成法を開発するのに年単位を要するというが、劇的に短い期間で実現されたのだ。
スパコン10年分の計算を短時間で
とはいえ、計算で発見された化学反応を実験で検証した例はまだ少ない。実験科学者の興味を引いて実験に至る例をこれから増やすには、より複雑で、現実的な化学反応をコンピューターで扱えるようにする必要がある。
ここでも高い壁として立ちはだかるのが計算コストの問題だ。反応に関わる原子の数が多ければ多いほど、計算コストも増えるからだ。
この課題を解決するため、前田さんがICReDDのPIで、ビッグデータ解析による分子の設計などに強みを持つアレクサンドル・ヴァーネックさんの研究グループと取組んできたのが、データ分析手法として近年のAIブームを支える機械学習の応用だ。
AFIR法に基づく反応経路自動探索では、量子化学的に厳密な密度汎関数理論（DFT）を用いて分子のエネルギーなどを計算する。DFTの精度は高いのだが、分子のサイズが大きくなると計算コストが急増する。
前田さんらが提案したのは、ニューラルネットワークポテンシャル（NNP）と呼ばれる機械学習モデルを訓練することで、DFTと同等の精度でありながら、計算コストを大幅に削減して分子のエネルギーなどを予測する仕組みだ。
DFTは分子の構造予測、安定性評価など化学のあらゆる分野で利用されるが、計算コストは高い。そのDFTを、NNPで置き換える動きは近年急速に進んでいる。しかし前田さんによれば、反応経路自動探索をターゲットにする場合、この置き換えがなかなかうまくいかなかったのだという。
「NNPは訓練データの範囲を外れた、未知の領域に対しては予測精度が急激に落ちるからです。物理的に不自然な分子構造まで安定だと見積もってしまいがちなのです」
この弱点を克服するため、ヴァーネックさんの研究グループのルーベン・ストウブさん（ICReDDの特任助教）が試みたのがΔ（デルタ）学習と呼ばれるアプローチだ。粗いエネルギー推定を行う半経験的手法（xTB）をベースに、そこからDFTとのズレだけをNNPで学習させる。この工夫により、NNPの適用範囲をDFTに近づけつつ、計算の高速性も維持できるようになった（図５）。
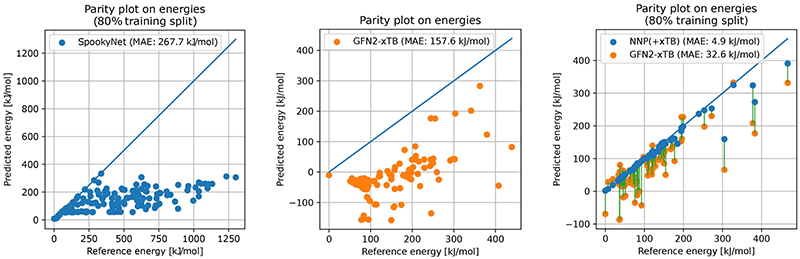図５）機械学習ポテンシャルの計算精度（エチレンの水素化反応の反応経路ネットワーク上の例）。NNP単体（左）、GFN2-xTB（中央）、そして、本研究で提案したNNP+xTBモデル（右、青い点）。
「網羅性と精度を維持して計算コストを下げるところに苦労しましたが、今はそのノウハウを確立し、100倍程度速く反応経路探索ができるようになりました」 NNPモデルを用いてAFIR法の計算コストを削減したことにより、これまで原子数20〜30個程度の分子しか現実的には扱えなかったところ、200個以上からなる分子まで扱えるようになった。
「たとえばICReDDのPIで、2021年にノーベル化学賞を受賞したベンジャミン・リスト先生のグループが開発している有機触媒の一つで、複雑な有機骨格を持ち、228個の原子からなるIDPi（イミドジホスホイミダート）に対してもNNPモデルとAFIR法により反応経路自動探索が現実的な時間で実行できました。もし同じ計算をDFTで実行したら、たとえば日本のスパコン富岳を使っても10年はかかるでしょうね」